ACCENTE NOI ÎN ANALIZA ŞI PROIECTAREA SISTEMELOR AUTOMATE
Prof. dr. ing . Sorin LARIONESCU – UTCB
Abordarea clasică în analiza şi proiectarea sistemelor automate se bazează pe schema bloc din Fig. 1. Se pune în evidenţă comparatorul şi funcţiile de transfer ale regulatorului, Hr , elementului de execuţie, He , procesului, Hp , şi traductorului, Ht . Semnalele de intrare sunt referinţa W şi perturbaţia V, iar ieşirea este Y. În interiorul sistemului automat sunt evidenţiate semnalele următoare: eroarea E, comanda U şi acţionarea M.
Fig. 1. Modelul unei bucle de reglare în abordarea clasică
În ultimii ani regulatoarele au devenit tot mai complexe realizând sarcini noi cu performanţe ridicate. O schemă bloc a unui sistem automat modern este prezentată în
Fig. 2. De data aceasta regulatorul cuprinde prefiltrul F, compensatorul erorii K, compensatorul perturbaţiei C şi două comparatoare. În privinţa instalaţiei se observă că se pune în evidenţă funcţia de transfer pe calea directă G, funcţia de transfer pe calea inversă H şi funcţia de transfer a perturbaţiei D.Fig. 2. Modelul unui sistem modern de reglare automată
Comparând Fig. 1 cu Fig. 2 se observă că funcţia de transfer pe calea directă G include elementul de execuţie şi procesul, iar funcţia de transfer pe calea inversă H corespunde traductorului. Modul diferit de modelare a instalaţiei prin blocuri funcţionale care apare în Fig. 2 este o consecinţă a mai multor fapte noi. În primul rând regulatorul are două grade de libertate. Compensatorul K al erorii este proiectat pentru funcţionarea în regim de reglare iar prefiltrul F este proiectat pentru funcţionarea în regim de urmărire. În al doilea rând, regulatorul are compensatorul C pentru înlăturarea efectelor perturbaţiei printr-o legătură feedforward. Şi în sfârşit, în al treilea rând, se ia în considerare în mod explicit zgomotul N care poate apare la ieşirea traductorului. Ca urmare a creşterii numărului de blocuri şi a folosirii proiectării asistate de calculator s-a renunţat la maniera de notare a tuturor funcţiilor de transfer cu litera H urmată de un indice (Fig. 1).
Pentru analiza şi proiectarea sistemului automat din
Fig. 2 se pune în evidenţă, în abordarea clasică, funcţiile de transfer H0R , H0P şi H0N ale referinţei, perturbaţiei şi zgomotului, ca în relaţia (1) . În privinţa notaţiei se observă că funcţiile de transfer cu bucla închisă se notează tot cu H, dar cu indicele 0.![]()
în care:
![]()
![]()
(3)
![]()
(4)
În lucrările recente, ca şi în multe din pachetele de programe, consacrate analizei şi proiectării sistemelor automate, relaţia
(1) este prezentată sub forma (5):![]()
în care S este funcţia de sensibilitate iar T este funcţia de sensibilitate complementară a sistemului automat şi sunt definite de relaţiile (6) şi (7).
![]()
![]()
Între T şi S există relaţia (8) care justifică denumirea de funcţie de sensibilitate şi funcţie de sensibilitate complementară.
Deşi
S şi T pot fi definite ca nişte funcţii de transfer, din denumirea lor se observă că accentul este pus pe o altă caracteristică, sensibilitatea a sistemului automat.O performanţă importantă a sistemelor este sensibilitatea la variaţia unui parametru α a funcţii de transfer
G(s, α). Indexul de performanţă Bode pentru sensibilitate este definit astfel: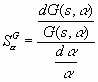
(9)
Aplicând indexul de sensibilitate Bode la funcţia de transfer
(2) a sistemului automat în regim de urmărire se obţine funcţia de sensibilitate S(s) (10) definită anterior de relaţia (7):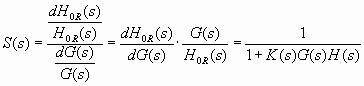
O urmărire ideală presupune
Y(s)=R(s), adică H0R(s)=1 sau E(s)=0, unde eroarea E(s) este:
Pentru o eroare nulă rezultă din
(11) că este necesar ca K(s)=∞, fapt imposibil. Mai mult, chiar valori mari ale lui K(s) nu sunt posibile în practică fără înrăutăţirea stabilităţii sistemului. In practică se acceptă performanţe mai puţin ambiţioase decât eroarea nulă, de exemplu criterii integrale sau anularea erorii numai în regim staţionar. Conform teoremei valorii finale eroarea indicială staţionară este definită în modul următor: ![]()
(12)
in care R1(s) este un semnal de referinţă tip treaptă unitară.
Folosirea unui regulator automat la conducerea instalaţiei prin închiderea buclei de reacţie negativă conduce la obţinerea sistemului automat din Fig. 2. Instalaţia automatizată are caracteristici remarcabile. Efectul perturbaţiei P(s) este înlăturat în mare măsură, funcţionarea este mai liniară şi sensibilitatea instalaţiei la modificarea parametrilor este scăzută. Sistemul automat răspunde mai rapid la semnalele de intrare. Preţul plătit pentru aceste beneficii ale automatizării constă în posibilitatea ca sistemul automat să devină instabil. Din această cauză rezerva de stabilitate, sau robusteţea sistemului, este performanţa sa cea mai importantă.
Abordarea clasică în aprecierea robusteţi unui sistem automat foloseşte indicatorii marginea de amplificare MA şi marginea de fază MF. Din păcate există situaţii în care aceşti indicatori nu dau informaţii corecte. Un exemplu va lămurii situaţia.
În Fig. 2 să considerăm funcţia de transfer (13) pentru partea fixă a instalaţiei şi funcţia de transfer (14) pentru compensatorul PID cu filtrare. Traductorul este considerat ideal H(s)=1.
![]()
![]()
Dacă notăm cu
L(s) funcţia de transfer (15) a sistemului cu bucla deschisă, atunci marginea de amplificare MA şi marginea de fază MF pot fi determinate pe diagrama Nyquist a lui L(jω) din Fig. 3.Marginea de amplificare MA este inversul distanţei de la origine la punctul de intersecţie a hodografului lui L(jω) cu axa reală şi reprezintă factorul cu care trebuie înmulţit modulul lui L(jω) pentru ca sistemul automat să devină instabil.
Marginea de fază
MF este unghiul dintre axa reală negativă şi dreapta care uneşte originea cu punctul de intersecţie a cercului unitar cu hodograful lui L(jω). Marginea de fază reprezintă defazajul suplimentar al lui L(jω) pentru ca sistemul automat să devină instabil.S-au stabilit empiric regulile (16) şi (17) pentru robusteţea sistemului automat.
Pentru exemplul considerat rezultă din
Fig. 3 o margine de amplificare MA=2,03 şi o margine de fază MF=83,5ş. Conform regulilor empirice (16)şi (17) sistemul automat este robust. Totuşi, se observă în Fig. 3 că hodograful lui L(jω) se apropie în mod periculos de punctul critic (-1, j0). Un indicator mai bun al robusteţii îl constituie deci această distanţă minimă, numită margine de modul MM, dintre hodograful lui L(jω) şi punctul critic.Marginea de modul MM este raza cecului cu centrul în punctul critic (-1, j0) şi tangent la hodograful lui L(jω). Vectorul care uneşte punctul critic (-1, j0) cu punctul cel mai apropiat de pe hodograful lui L(jω) are modulul dat de relaţia (18)
![]()
O nouă definiţie
(20) a marginii de modul MM rezultă din relaţiile (18) şi (19).
![]()
în care |S(jω)|max este valoarea cea mai mare dintre vârfurile modului lui S(jω).
Ca şi în cazul marginii de amplificare sau a marginii de fază există o regulă empirică (21) pentru valoarea marginii de modul MM care asigură robusteţea sistemului automat.
Marginea de modul se calculează uşor cu relaţia
(20). Pentru exemplul considerat modulul funcţiei de sensibilitate este prezentat în Fig. 4. Valoarea sa maximă este 2,14 şi deci rezultă din (20) valoarea MM = 0,467. Deci sistemul automat nu îndeplineşte condiţia (21) şi nu este robust. Această concluzie coincide şi cu situaţia vizibilă în Fig. 3.Condiţia de robusteţe
(21) implică şi realizarea condiţiilor de robusteţe (16) şi (17). După cum am văzut din exemplul prezentat reciproca nu este valabilă.Fig. 4. Determinarea marginii de amplificare MA, marginii de fază MF şi a marginii de modul MM.
Creşterea unor performanţe ale sistemului automat implică uneori micşorarea robusteţi sale. Marginea de modul este cel mai bun indicator al faptului că o anumită limită a robusteţii, de exemplu cea indicată de relaţia
(21), nu este depăşită.Accentuarea din ultimul timp a importanţei funcţiei de sensibilitate
S în analiza şi proiectarea sistemelor automate este justificată de rolul important pe care aceasta îl joacă în transferul perturbaţiei la ieşire, în determinarea robusteţi, sensibilităţii şi erorii indiciale staţionare.Bibliografie